[알고리즘 Python] BFS, DFS
DFS
Dept-First Search, 깊이 우선 탐색 알고리즘
그래프의 기본 구조, 표현 방식
그래프틑 Node, Edge로 표현이 되며 이때 Node를 Vetex라고도 말한다.
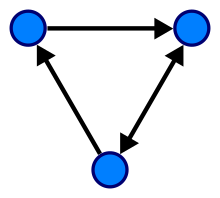
- 인접 행렬 : 2차원 배열로 그래프의 연결 관계를 표현하는 방식
연결되어 있지 않은 노드끼리는 INF 비용이라고 작성한다. 999,999,999로 초기화 하는 경우가 많다.
INF = 999999999
graph = [
[0, 7, 5]
[7, 0, INF]
[5, INF, 0]
]
- 인접 리스트
모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장한다.
C++에서는 라이브러리를 이용하여 연결 리스트의 자료구조를 이용해 구현한다.
반면에 파이썬은 리스트를 그냥 이용한다. 파이썬으로 인접리스트를 표현하고자 할 때에도 단순히 2차원 리스트를 이용한다.
graph = [[] for _ in range(3)]
graph[0].append((1, 7)) # (노드, 거리)
graph[0].append((2, 5))
graph[1].append((0, 7))
graph[2].append((0, 5))
print(graph)
- 메모리, 속도 측면에서 바라본 인접 행렬 vs 인접 리스트
인접 행렬 방식 : 모든 관계를 저장하므로 메모리를 많이 잡아먹으나, 속도는 빠르다.
인접 리스트 방식 : 메모리를 적게 잡아 먹으나, 속도는 느리다.
DFS 동작과정
DFS는 스택 자료구조를 이용
- 탐색 시작 노드를 스택에 삽입하고 방문 처리
- 방문하지 않은 (최대한 작은 노드부터, 순서가 더 빠른 노드부터) 인접 노드가 있으면 그 노드를 스택에 넣고 방문 처리. 없으면 pop, 최상단 노드를 꺼낸다.
- 1, 2 를 반복
DFS는 스택 자료구조에 기초하고, 데이터의 개수가 N개인 경우 $O(N)$의 시간이 소요된다는 특징을 가진다.
-> 구현할때는 스택 자료구조를 사용하지 않고 재귀함수를 이용한다
예제 코드
def dfs(graph, v, visited):
visited[v] = True
print(v, end=' ')
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visitied = [False] * 9
dfs(graph, 1, visited)
BFS
Breadth First Search ‘너비 우선 탐색’ : 가까운 노드부터 탐색하는 알고리즘이다.
큐 자료구조를 이용하는 것이 정석이다.
BFS 동작과정
- 탐색 시작 노드를 큐에 삽입하고 방문 처리
- 인접 노드 중에서 방문하지 않은 노드를 모드 큐에 삽입하고 방문처리 (작은 노드, 우선순위가 더 빠른 노드부터 큐에 삽입)
- 1, 2번 과정 반복
실제로 구현은 deque 라이브러리를 사용한다. DFS와 마찬가지로 $O(N)$의 시간이 소요되지만 일반적인 경우 실제 수행시간은 DFS보다 좋은 편이다.
from collections import deque
def bfs(graph, start, visited):
queue = deque([start])
visited[start] = True
while queue:
v = queue.popleft()
print(v, end= ' ')
for i in graph[v]:
if not visited[i]:
queue.append(i)
visitied[i] = True
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visitied = [False] * 9
bfs(graph, 1, visited)
문제
음료수 얼려 먹기
n, m = map(int, input().split())
graph = []
for i in range(n):
graph.append(list(map(int, input())))
def dfs(x, y):
if x <= -1 or x >= n or y <= -1 or y >= m:
return False
if graph[x][y] == 0:
graph[x][y] = 1
dfs(x - 1, y)
dfs(x, y - 1)
dfs(x + 1, y)
dfs(x, y + 1)
return True
return False
result = 0
for i in range(n):
for j in range(m):
if dfs(i, j) == True:
result += 1
print(result)
dfs를 이용하여 해결할 수 있다. dfs가 비교적 조건이 없을 때 더 간단하게 해결할 수 있다. 여기서 핵심은 초기 시작위치만 카운트를 해주고 나머지 연결된 노드는 방문처리(1로) 해주는 것이다.
미로 탈출
from collections import deque
n, m = map(int, input().split())
graph = [list(map(int, input().split())) for _ in range(n)]
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
def bfs(x, y):
queue = deque()
queue.append((x, y))
while queue:
x, y = queue.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx < 0 or ny < 0 or nx >= n or ny >= m:
continue
if graph[nx][ny] == 0:
continue
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1
queue.append((nx, ny))
return graph[n - 1][m - 1]
print(bfs(0, 0))
최소경로를 구하는 문제이므로 bfs가 더 적합한 거 같다.
아직 감이 제대로 안잡히므로 문제좀 더 풀어봐야 할 것 같다.

댓글남기기